| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 다익스트라
- 크루스칼
- django
- 프로그래머스
- 코딩테스트
- 그래프 탐색
- Database
- 최단경로
- AWS
- 피로그래밍
- SQL
- Pirogramming
- 누적합
- OrderBy
- MST
- JOIN
- Baekjoon
- 배포
- union find
- BFS
- EC2
- SQL코딩테스트
- GROUPBY
- 자바
- 프림
- db
- Java
- 알고리즘
- 구현
- 백준
- Today
- Total
NullNull
[백준 P14621] 나만 안되는 연애 Java 본문
P14621 나만 안되는 연애
14621번: 나만 안되는 연애
입력의 첫째 줄에 학교의 수 N와 학교를 연결하는 도로의 개수 M이 주어진다. (2 ≤ N ≤ 1,000) (1 ≤ M ≤ 10,000) 둘째 줄에 각 학교가 남초 대학교라면 M, 여초 대학교라면 W이 주어진다. 다음 M개의
www.acmicpc.net
문제
깽미는 24살 모태솔로이다. 깽미는 대마법사가 될 순 없다며 자신의 프로그래밍 능력을 이용하여 미팅 어플리케이션을 만들기로 결심했다. 미팅 앱은 대학생을 타겟으로 만들어졌으며 대학교간의 도로 데이터를 수집하여 만들었다.
이 앱은 사용자들을 위해 사심 경로를 제공한다. 이 경로는 3가지 특징을 가지고 있다.
- 사심 경로는 사용자들의 사심을 만족시키기 위해 남초 대학교와 여초 대학교들을 연결하는 도로로만 이루어져 있다.
- 사용자들이 다양한 사람과 미팅할 수 있도록 어떤 대학교에서든 모든 대학교로 이동이 가능한 경로이다.
- 시간을 낭비하지 않고 미팅할 수 있도록 이 경로의 길이는 최단 거리가 되어야 한다.
만약 도로 데이터가 만약 왼쪽의 그림과 같다면, 오른쪽 그림의 보라색 선과 같이 경로를 구성하면 위의 3가지 조건을 만족하는 경로를 만들 수 있다.
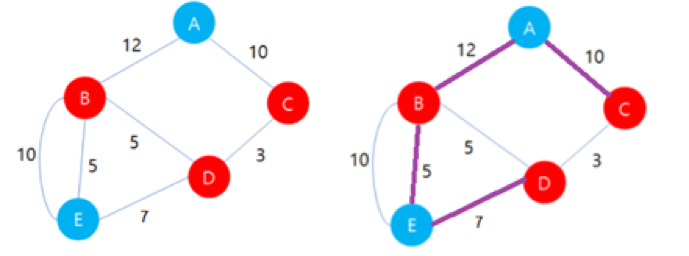
이때, 주어지는 거리 데이터를 이용하여 사심 경로의 길이를 구해보자.
입력값
입력의 첫째 줄에 학교의 수 N와 학교를 연결하는 도로의 개수 M이 주어진다. (2 ≤ N ≤ 1,000) (1 ≤ M ≤ 10,000)
둘째 줄에 각 학교가 남초 대학교라면 M, 여초 대학교라면 W이 주어진다.
다음 M개의 줄에 u v d가 주어지며 u학교와 v학교가 연결되어 있으며 이 거리는 d임을 나타낸다. (1 ≤ u, v ≤ N) , (1 ≤ d ≤ 1,000)
5 7
M W W W M
1 2 12
1 3 10
4 2 5
5 2 5
2 5 10
3 4 3
5 4 7
출력값
깽미가 만든 앱의 경로 길이를 출력한다. (모든 학교를 연결하는 경로가 없을 경우 -1을 출력한다.)
34
알고리즘
24살 모태솔로 깽미를 도와주자.
사심 경로가 이어지기 위해서는 남초 대학교는 여초 대학교와, 여초 대학교는 남초 대학교와 연결되어야 한다. 그리고 경로의 길이는 최단 거리가 되어야 한다.
모든 대학교가 연결되어야 하고, 그 거리가 최단 거리가 되어야 하므로 MST를 이용하면 풀 수 있는 문제이다. 그러나 한 가지 조건이 추가되었기에 이를 구현해야 한다.
알고리즘은 크루스칼 알고리즘을 사용했다. 간선의 정보를 저장하고 현재 가지고 있는 간선들 (아직 탐색하지 않은) 중 가장 작은 가중치를 가지는 간선을 뽑아낸다.
그 간선에 연결된 양 끝의 두 노드가 서로 다른 종류의 학교일 때만 간선으로 등록하기 위해 union 해준다.
즉, 남초 대학교와 남초 대학교가 연결된 간선이라면 간선으로 등록하지 않고, 여초 대학교와 남초 대학교 처럼 다른 종류의 대학교가 연결되는 경우에만 간선으로 등록한다.
간선을 등록한 횟수가 N - 1회가 된다면 MST가 구성된 것이므로 가중치의 합을 출력한다. N - 1개보다 적은 횟수로 간선의 등록이 일어났다면, 경로가 없는 경우로 판단하고 -1을 출력한다.
전체 코드는 다음과 같다.
코드
import java.util.*;
import java.io.*;
public class Main {
static int N, M, answer;
static int[][] parent;
static PriorityQueue<int[]> edges;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
st = new StringTokenizer(br.readLine());
parent = new int[N + 1][2];
for (int i = 1; i <= N; i++) {
parent[i][0] = i;
parent[i][1] = st.nextToken().charAt(0) - 'M' == 0 ? 0 : 1;
}
edges = new PriorityQueue<>((a, b) -> {
return Integer.compare(a[2], b[2]);
});
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
edges.add(new int[] {from, to, weight});
}
int n = 0;
while (!edges.isEmpty()) {
int[] current = edges.poll();
int from = current[0];
int to = current[1];
int weight = current[2];
if (find(from) == find(to)) continue;
if (parent[from][1] == parent[to][1]) continue;
union(from, to);
n++;
answer += weight;
if (n == N - 1) {
break;
}
}
System.out.println(n == N - 1 ? answer : -1);
}
public static void union(int a, int b) {
int aParent = find(a);
int bParent = find(b);
if (aParent < bParent) parent[bParent][0] = aParent;
else if (bParent < aParent) parent[aParent][0] = bParent;
}
public static int find(int target) {
if (parent[target][0] == target) return target;
else return parent[target][0] = find(parent[target][0]);
}
}
'알고리즘' 카테고리의 다른 글
| [백준 P15681] 트리와 쿼리 Java (0) | 2022.11.11 |
|---|---|
| [백준 P21924] 도시 건설 Java (0) | 2022.11.03 |
| [백준 P23634] 미안하다 이거 보여주려고 어그로 끌었다 Java (0) | 2022.11.01 |
| [백준 P3197] 백조의 호수 Java (0) | 2022.10.29 |
| [백준 P11403] 경로 찾기 Java (1) | 2022.10.29 |




