| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- JOIN
- db
- SQL
- 최단경로
- 프로그래머스
- GROUPBY
- 코딩테스트
- 크루스칼
- OrderBy
- 피로그래밍
- Java
- 백준
- 그래프 탐색
- 자바
- 누적합
- BFS
- 프림
- Baekjoon
- Database
- union find
- django
- 배포
- 구현
- Pirogramming
- 알고리즘
- EC2
- MST
- 다익스트라
- SQL코딩테스트
- AWS
- Today
- Total
NullNull
[백준 P10423] 전기가 부족해 Java 본문
P10423전기가 부족해
10423번: 전기가 부족해
첫째 줄에는 도시의 개수 N(1 ≤ N ≤ 1,000)과 설치 가능한 케이블의 수 M(1 ≤ M ≤ 100,000)개, 발전소의 개수 K(1 ≤ K ≤ N)개가 주어진다. 둘째 줄에는 발전소가 설치된 도시의 번호가 주어진다. 셋째
www.acmicpc.net
문제
세계에서 GDP가 가장 높은 서강 나라는 소프트웨어와 하드웨어 기술이 모두 최고라서 IT강국이라 불리고, 2015년부터 세상에서 가장 살기 좋은 나라 1등으로 꼽히고 있다.
살기 좋은 나라 1등으로 꼽힌 이후 외국인 방문객들이 많아졌고, 그에 따라 전기 소비율이 증가하여 전기가 많이 부족한 상황이 되었다. 따라서 서강 나라의 대통령은 최근 개발이 완료된 YNY발전소 프로젝트를 진행 하기로 하였다. 발전소를 만들 때 중요한 것은 발전소 건물과 도시로 전기를 공급해 줄 케이블이다. 발전소는 이미 특정 도시에 건설되어 있고, 따라서 추가적으로 드는 비용은 케이블을 설치할 때 드는 비용이 전부이다. 이 프로젝트의 문제는 케이블을 설치할 때 드는 비용이 굉장히 크므로 이를 최소화해서 설치하여 모든 도시에 전기를 공급하는 것이다. 여러분은 N개의 도시가 있고 M개의 두 도시를 연결하는 케이블의 정보와 K개의 YNY발전소가 설치된 도시가 주어지면 케이블 설치 비용을 최소로 사용하여 모든 도시에 전기가 공급할 수 있도록 해결해야 한다. 중요한 점은 어느 한 도시가 두 개의 발전소에서 전기를 공급받으면 낭비가 되므로 케이블이 연결되어있는 도시에는 발전소가 반드시 하나만 존재해야 한다. 아래 Figure 1를 보자. 9개의 도시와 3 개의 YNY발전소(A,B,I)가 있고, 각각의 도시들을 연결할 때 드는 비용이 주어진다.

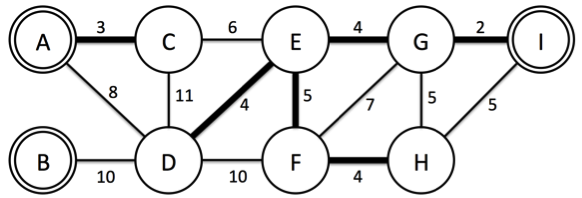
이 예제에서 모든 도시에 전기를 공급하기 위하여 설치할 케이블의 최소 비용은 22이고, Figure 2의 굵은 간선이 연결한 케이블이다. B 도시는 연결된 도시가 하나도 없지만, 발전소가 설치된 도시는 전기가 공급될 수 있기 때문에 상관없다.
입력값
첫째 줄에는 도시의 개수 N(1 ≤ N ≤ 1,000)과 설치 가능한 케이블의 수 M(1 ≤ M ≤ 100,000)개, 발전소의 개수 K(1 ≤ K ≤ N)개가 주어진다. 둘째 줄에는 발전소가 설치된 도시의 번호가 주어진다. 셋째 줄부터 M개의 두 도시를 연결하는 케이블의 정보가 u, v, w로 주어진다. 이는 u도시와 v도시를 연결하는 케이블을 설치할 때 w의 비용이 드는 것을 의미한다. w는 10,000보다 작거나 같은 양의 정수이다.
9 14 3
1 2 9
1 3 3
1 4 8
2 4 10
3 4 11
3 5 6
4 5 4
4 6 10
5 6 5
5 7 4
6 7 7
6 8 4
7 8 5
7 9 2
8 9 5
4 5 1
1
1 2 5
1 3 5
1 4 5
2 3 10
3 4 10
10 9 5
1 4 6 9 10
1 2 3
2 3 8
3 4 5
4 5 1
5 6 2
6 7 6
7 8 3
8 9 4
9 10 1
출력값
모든 도시에 전기를 공급할 수 있도록 케이블을 설치하는 데 드는 최소비용을 출력한다.
22
15
16
알고리즘
모든 도시에 전기를 공급할 수 있게 함과 동시에, 어느 한 도시가 두 개의 발전소에서 전기를 공급받으면 안되므로 MST 문제임을 유추할 수 있다.
MST 는 크루스칼과 프림 두 가지 알고리즘으로 풀 수 있다. 이번 문제는 정점은 1000개임에 반해, 케이블 수 (엣지) 가 100000개 이다. 정점보다 엣지의 수가 더 많기 때문에, 크루스칼 보다 프림 알고리즘을 활용하여 문제를 풀이했다.
입력으로 들어오는 형식에 맞게 그래프를 인접리스트 방식으로 저장하고, 이미 발전소가 있는 도시는 연결되어 있다고 판단하고 visited를 true로 바꾸어주었다. 그리고 발전소에 인접한 정점과 발전소부터 그 정점까지의 거리를 각각 저장하는 int 배열을 우선순위 큐에 넣어주었다.
int cnt = 0;
long total = 0;
for (int e: electric) {
visited[e] = true;
for (int[] next: graph[e]) {
pq.add(next);
}
cnt++;
}
이후에 우선순위 큐에서 하나씩 큐안에서 가장 짧은 거리를 가지는 정점을 뽑아낸 뒤, 이미 방문한 적이 있는 정점인지 확인하고, 방문되지 않은 정점이라면 visited를 true로 바꾸고 그 정점에 인접한 다른 정점들 중 연결해야하는 정점만 추가로 우선순위 큐에 넣어주었다.
while (!pq.isEmpty()) {
int[] current = pq.poll();
int curPlace = current[0];
int curWeight = current[1];
if (!visited[curPlace]) {
visited[curPlace] = true;
total += curWeight;
cnt++;
for (int[] next: graph[curPlace]) {
if (!visited[next[0]])
pq.add(next);
}
}
if (cnt == N) {
break;
}
}
만약 모든 정점이 다 연결되었다고 판단되면 반복문을 종료하고 total 값을 출력한다.
전체 코드는 아래와 같다.
코드
import java.util.*;
import java.io.*;
public class Main {
static int N, M, K;
static List<int[]>[] graph;
static int[] electric;
static boolean[] visited;
static PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> {
return Integer.compare(a[1], b[1]);
});
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
electric = new int[K];
visited = new boolean[N + 1];
graph = new ArrayList[N + 1];
for (int i = 1; i <= N; i++) {
graph[i] = new ArrayList<>();
}
st = new StringTokenizer(br.readLine());
for (int i = 0; i < K; i++) {
electric[i] = Integer.parseInt(st.nextToken());
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int weight =Integer.parseInt(st.nextToken());
graph[from].add(new int[] {to, weight});
graph[to].add(new int[] {from, weight});
}
int cnt = 0;
long total = 0;
for (int e: electric) {
visited[e] = true;
for (int[] next: graph[e]) {
pq.add(next);
}
cnt++;
}
while (!pq.isEmpty()) {
int[] current = pq.poll();
int curPlace = current[0];
int curWeight = current[1];
if (!visited[curPlace]) {
visited[curPlace] = true;
total += curWeight;
cnt++;
for (int[] next: graph[curPlace]) {
if (!visited[next[0]])
pq.add(next);
}
}
if (cnt == N) {
break;
}
}
System.out.println(total);
}
}
'알고리즘' 카테고리의 다른 글
| [백준 P11779] 최소비용 구하기 2 자바 Java (0) | 2022.12.07 |
|---|---|
| [백준 P1916] 최소비용 구하기 자바 Java (0) | 2022.12.07 |
| [백준 P15681] 트리와 쿼리 Java (0) | 2022.11.11 |
| [백준 P21924] 도시 건설 Java (0) | 2022.11.03 |
| [백준 P14621] 나만 안되는 연애 Java (1) | 2022.11.03 |


